Intervista a Narciso Silvestrini / L'ordine dei colori
Narciso Silvestrini è un maestro del colore: è stato docente all’Istituto Statale d’arte di Monza (ora Liceo Artistico Nanni Valentini), una scuola sperimentale nella quale ha insegnato per oltre 20 anni, alla Scuola del Libro all’Umanitaria di Milano, al Politecnico di Milano e alla Scuola Politecnica di Design di Milano. Nel 1986 ha curato per la Biennale di Venezia il tema Colour Order Systems e possiamo trovare le tavole esposte, accanto ad altre che ne ampliano il complesso quadro, nel volume inglese Color Systems in Art and Science (Regenbogen Verlag, Konstanz 1996) oppure nel testo Farbsysteme in Kunst und Wissenschaft (DuMont, Köln 1998), pubblicati in collaborazione con Ernst Peter Fisher. Le tavole originali, raccolte in volume, si trovano al Bauhaus-Archiv di Berlino.
Credo che mettere ordine nel mondo dei colori derivi da una curiosità che tutti abbiamo avuto fin da bambini quando abbiamo dovuto sistemare le matite in un astuccio e non sapevamo dove mettere il rosa e l’arancione. Questa sistemazione lineare non assomiglia ai primi criteri di ordinamento? Si pongono agli estremi il bianco e il nero, dalla giustapposizione dei quali si fanno scaturire tutti gli altri colori, un po’, forse, come aveva pensato Aristotele. Quali sono le difficoltà e incongruenze di una rappresentazione lineare?
Intorno agli anni Sessanta uno degli argomenti in discussione sul colore (Deane Brewster Judd e altri) era, come riportano Fred W. Billmeyer jr. e Max Saltzman, quello denominato “desert island”. Una persona, priva di precedenti cognizioni in merito, si trova in un deserto, in mezzo a una distesa di sassolini di vari colori. Quali criteri visivi adottare per ordinare tanta varietà? Noi diremmo: per separazione tra colori cromatici e colori acromatici? per tinta? per chiarezza? per saturazione? per somiglianza o prossimità di tinte? come disporre poi i sassolini all’interno di ciascun gruppo selezionato?
Il criterio privilegiato sembrerebbe quello lineare, dal momento che la linea, la scala, è continua, è obbligata, progressiva, gerarchica, di immediata e univoca lettura, a differenza della mappa, della tavola, della rete, dell’atlante, dell’albero, della sfera... (Giulio Barsanti) e lineari sono le disposizioni dei colori da parte di Aristotele, di Leonardo Da Vinci, di Franciscus Aguilonius, di Athanasius Kircher, ...
Ma la disposizione lineare è poi la più semplice, congruente, esaustiva?
Dipende. Si prenda, ad esempio, il cubo, nel caso il cubo dei colori RGB-CMY-WK. Qui la linea più semplice è quella, monodimensionale, dei suoi spigoli; meno semplici sono le dodici diagonali delle sue sei facce, in quanto ciascuna di esse risulta dalla composizione di due vettori o spigoli; più complesse ancora sono le sue quattro diagonali interne risultante ciascuna dalla composizione di tre vettori o spigoli.
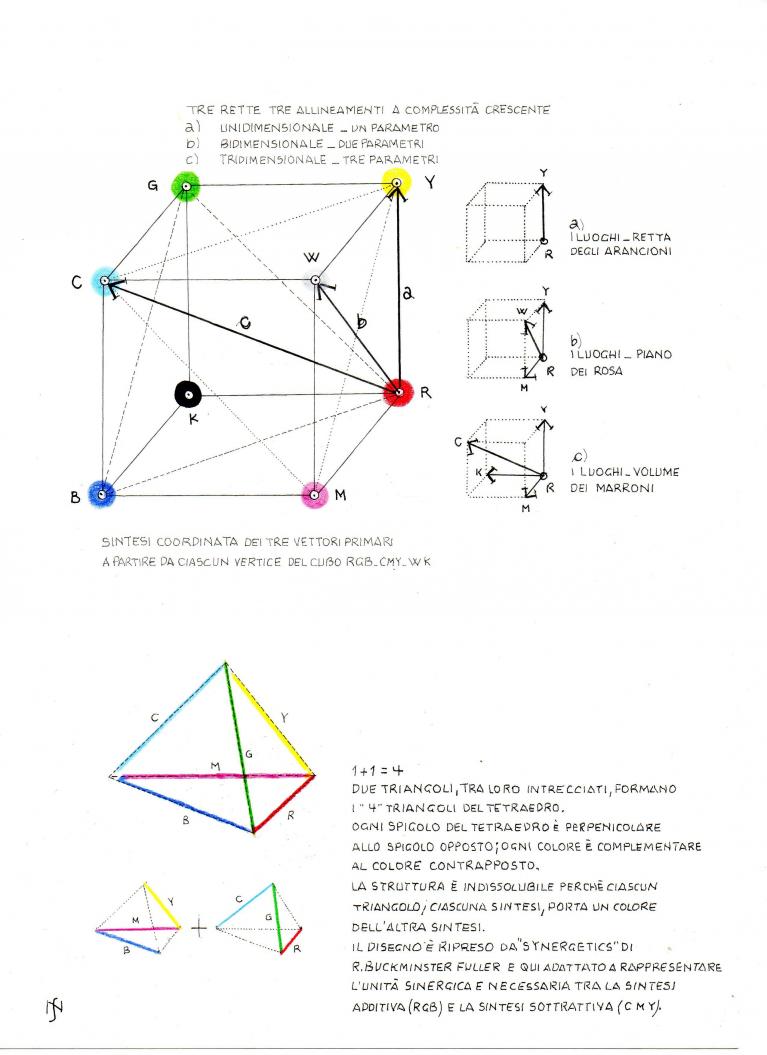 sistemi vettoriali
sistemi vettoriali
Ora, con riferimento ai suoi esempi, non è difficile collocare l’arancione, dal momento che è situato su uno spigolo del cubo, quello giallo-rosso; più difficile disporre i rosa perché ubicati su un piano e quindi sintesi di due vettori o parametri; più difficile ancora posizionare i marroni, i bruni, i verde oliva, perché stanno sospesi nello spazio cubico e quindi sono sintesi di tre parametri (tinta, chiarezza, saturazione).
Penso che la propensione prima ad allineare consegua dal fatto che noi possiamo vedere solo una cosa alla volta per poi trascorrere da cosa a cosa; lineari sono anche il parlare, lo scrivere, il camminare ... È interessante rilevare che anche nella numerazione si faccia distinzione tra numeri cardinali (il fissare) e numeri ordinali (lo scorrere).
L’ordinare risulta più difficile se i colori da disporre sono pochi (troppa differenza) oppure sono tanti (poca differenza) come possiamo verificare osservando, come lei fa notare, le piccole o grandi scatole di matite colorate esposte, aperte, in vetrina.
Nel libro sui sistemi del colore lei afferma che il primo sistema geometrico dei colori risale al Seicento. Da allora sono stati elaborati diversi modelli geometrici; la differenza principale dei sistemi proposti nell’Ottocento mi sembra da ricondurre alla scelta di tre oppure quattro colori fondamentali. La soluzione dei quattro colori, proposta dal fisiologo Ewald Hering, sembra più corrispondente al fatto che noi non possiamo vedere, né immaginare, un giallo che dà sul blu o un rosso che dà sul verde.
Si ritiene che il primo modello “sistema colore” sia quello proposto da Sigerio Forsius (1611), professore di astronomia. Con tutta probabilità si tratta di una sfera, ordinata su 4 + 1 colori detti “fondamentali”:
rosso giallo (grigio) verde blu
compresi, ancora una volta, tra gli estremi bianco e nero (Ernst Peter Fischer). Tutti i successivi modelli, pur differenti tra loro per concezione e finalità potrebbero essere unitariamente relazionati tra loro disponendoli lungo i lati dello storico triangolo pitagorico “3-4-5”: un triangolo singolare, basato non sul criterio di uguaglianza, ma su quello di equivalenza.
– sul lato di misura “3” i sistemi trivarianti: Runge, Goethe, Young, Helmholtz, RGB-CMY, CIE ...
– sul lato di misura “4” i sistemi tetravarianti: Ostwald, DIN, Hering, NCS, OSA ...
– sul lato di misura “5” i sistemi pentavarianti: Kircher, Fludd, Munsell ...
Tracciando ora una circonferenza su ciascuno dei tre lati-sistema, presi come diametri, si ottiene una configurazione che può essere inscritta in un quadrato di misura “6”, tangente alle tre circonferenze e dove si può riscontrare l’intera modulazione
1–2–3–4–5–6
Con il “6” l’opera si completa: il “6” è il primo e solo numero perfetto.
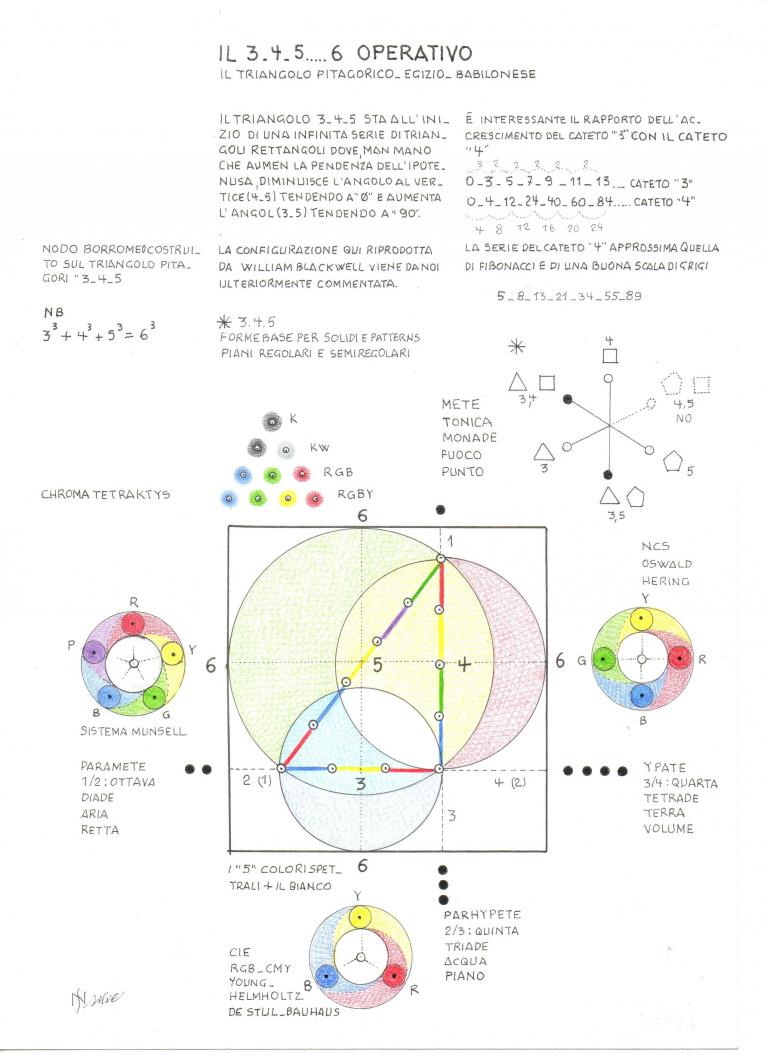 Il 3 - 4 - 5 - 6
Il 3 - 4 - 5 - 6
Nota a margine: Il prodotto fattoriale 1 x 2 x 3 x 4 x 5 x 6 = 720: è la somma, caratterizzante, degli angoli intorno ai quattro vertici del tetraedro; il tetraedro è il primo dei solidi e viene considerato come il “quanto” spaziale: tutti i solidi possono essere espressi in tetraedri (Richard Buckminster Fuller). Parimenti: il prodotto fattoriale (3 x 4 x 5) 3 = 180: la somma degli angoli interni del triangolo piano: il triangolo come “quanto” della superficie. La somma di quattro triangoli equilateri piani costruisce il tetraedro. In modo analogo a quello dei sistemi di colore, anche il sistema dei tre poligoni primari – triangolo (3), quadrato (4), pentagono (5) – può essere disposto sui corrispondenti lati del triangolo pitagorico ottenendo, dalle loro combinazioni, nel piano e nello spazio, tutte le configurazioni geometriche regolari e semiregolari.
Quindi non solo tre o quattro colori fondamentali, ma anche cinque. A questo si aggiunge la possibilità di trovare un’equivalenza, una specie di analogia, tra i vari sistemi dei colori in una sorta di meta-sistema. Come funziona, in questo contesto, la scala dei grigi? La scelta di Philipp Otto Runge di costruire la sfera, aggiungendo la terza dimensione, risolve il problema di far interagire la scala dei colori con la scala dei grigi?
La scala neutra dei grigi può risultare da due processi: dalla sintesi di opposte tinte, ma di uguale chiarezza, oppure da un progressivo venir meno del tenore di bianco, da un processo che Roberto Grossatesta chiama di “remissione”. Così si può dire che il bianco scende ai colori per “remissione” e il nero ascende ai colori per “intenzione”.
Come può la scala dei grigi derivare dalla mescolanza progressiva del bianco con il nero, dalla mescolanza cioè di due assoluti? a me non pare possibile. D’altra parte il fatto che la scala ottenuta per remissione risulti più lunga di quella per riduzione degli opposti, dipendente dalla circostanza che nessuna tinta può divenire chiara quanto il bianco o scura quanto il nero, dimostra sia la doppia origine della scala dei neutri, sia, a volte, la collocazione del polo bianco e del polo nero fuori dal cerchio delle tinte (Kandinskij), sia anche la doppia opinione se il bianco e il nero siano colori oppure no; naturalmente occorre premettere la definizione di “colore”.
Il grigio, la chiarezza, pervade l’intero spazio cromatico: ogni tinta ha il proprio grigio purché di pari chiarezza, ad ogni grigio corrispondono tutte le tinte di pari chiarezza. È per questo che è possibile “tradurre” un’immagine a colori in una corrispondente, ma non equivalente, immagine in bianco e nero, ma non viceversa. Penso che la chiarezza, presente dappertutto, abbia il compito di tener unite le diversità visive del mondo e le tinte, viceversa, di distinguere una cosa dall’altra. Le tinte stanno alla chiarezza come, in aritmetica, i numeratori stanno al denominatore. L’asse dei neutri è il luogo dove gli opposti risolvono, o nascondono, in un tertium la loro contesa, altrimenti catastrofica. L’antagonismo, la contraddizione, che caratterizza la seconda parte del processo visivo, impedisce la catastrofe non consentendo di vedere, e nemmeno di immaginare, un rosso–verde o un giallo–blu... e rende enigmatico il quesito: se posso tracciare la stessa linea con una matita blu, rossa, verde, perché non posso tracciare una linea blu con una matita rossa o gialla o ...? Mi spiego: mentre la linea (qualità primaria) permane tale al variare del suo colore, i colori (qualità secondarie) possoni sì variare, ma non sono tra loro intercambiabili, pena una variazione di senso.
Per quanto riguarda la sfera dei colori di Philipp Otto Runge, essa risolve o illustra la sinergia tra cromatici e acromatici, ma forse – e ricordo un’interessante mostra sulla sfera o meglio sulla sferitudine (Lugano 2006) – dico forse, è meno un modello di ordinamento materiale dei colori e più un archetipo poetico, un simbolo dell’esprit sphérique.
Nell’uso del computer ci siamo abituati a considerare come risolutivo il sistema RGB, basato sulla sintesi additiva, rosso, verde e blu, e fondato sul sistema internazionale di notazione del colore CIE (Commission internationale de éclairage). Questo sistema viene spesso identificato con il funzionamento della retina, ma la fisiologia ci dice che i coni sono sì di tre tipi, qualcuno più sensibile ai rossi, altri ai verdi, altri ancora ai blu; tutti, però, rispondono a tutte le lunghezze d’onda. Allora nemmeno il sistema CIE sembra catturare il mondo dei colori.
Se si osserva il diagramma di cromaticità CIE si può rilevare che esso presenta, più o meno estese e diversamente orientate, delle isole in forma di ellissi (ellissi di David Lewis Mac Adam e di Walter Stanley Stiles) all’interno delle quali non vi è, per la media degli osservatori discriminazione visiva, ossia tutti i punti interni a ciascuna ellisse sembrano tra loro cromaticamente uguali. Tali ellissi sono piuttosto piccole e frequenti nelle regioni del rosso e del blu, relativamente ampie nella regione del verde. Di contro nello spazio geometrico cartesiano entro il quale è disposto il diagramma CIE, ciascun punto ha coordinate diverse, ogni punto è diverso da tutti gli altri. Riassumendo, lo spazio cartesiano è continuo, omogeneo, infinito, lo spazio cromatico non è omogeneo, non è continuo, non è infinito. Detto diversamente, la lunghezza del metro cromatico è elastica e varia da colore a colore, mentre il metro del sistema internazionale (SI) è rigido e permane costante in ogni parte dello spazio ordinario.
Vani sono stati i tentativi, durati quasi cinquant’anni, di ridurre le ellissi a circonferenze tutte della stessa dimensione e distribuzione (UC, Uniform Chromaticity Scales) e rendere così commensurabili tra loro lo spazio cromatico e lo spazio geometrico. Non ho competenze per trattare delle proprietà strutturali e funzionali del sistema visivo ma, rifacendomi a quanto altri hanno osservato, il processo comincerebbe per “3”, con l’interazione (Young-Helmholtz) e arriverebbe a destinazione per “4”, con l’opposizione (Hering), per l’aggiunta del giallo: sintesi additiva del rosso e del verde. Sintesi che avverrebbe già nella retina dove il processo visivo passa, ergonomicamente, dall’analogico al digitale, ma è del tutto digitale dato che l’immagine viene inoltrata, convertita, lungo il nervo ottico e oltre mediante fibre nervose tra loro distinte? Sezionando i condotti si può ricavare una qualche “immagine”, componendo gli impulsi simultanei che stanno passando in quel momento lungo ciascuna fibra.
La sua indagine sui sistemi dei colori è davvero sorprendente e rivela una pluralità di soluzioni inaspettata e le forme di ordinamento sembrano davvero bizzarre. Forse ha ragione Hermann von Helmholtz che, in alcuni suoi articoli del 1891, scrive che il sistema dei colori richiede una geometria non euclidea?
La varietà, anche “bizzarra” dei modelli di colore testimonia i tentativi storici di dare forma coerente allo spazio cromatico. Alle volte è la suggestione della geometria a costringere il colore, altre volte è il colore che obbliga la geometria a inseguirlo nelle sue evoluzioni: due discipline tra loro adiacenti, ma con anche reciproci rimandi e inviti. Penso ad esempio, in geometria proiettiva, alla dualità tra il teorema di Pascal e il teorema di Brianchon, relativi alle coniche, che, se estesi, portano a riflettere sulla convergenza tra l’interno e l’esterno verso il confine comune, sulla definizione delle forme per luoghi o per inviluppo, sulla dualità tra il radiale e il tangenziale. Anche il colore dei corpi risulta per interazione tra il radiale della loro materia e il tangenziale dell’energia che li inviluppa. Penso al teorema cosiddetto del “quarto armonico”, relativo ai birapporti geometrici, secondo il quale, se un punto (c) si trova al centro di un intervallo (a-b), il suo corrispondente armonico (d) si trova all’infinito (d); un non luogo, necessario, ma immateriale.
Per traslazione, poiché il verde – il colore di Newton – si trova al centro dello spettro visivo rosso-violetto (R-V), il suo corrispondente armonico, il porpora – il colore di Goethe – dovrà trovarsi all’infinito; il porpora, un colore necessario, ma immateriale, un colore dell’altro mondo.
Quelli del colore sono modelli finiti, ma aperti, tendenti all’infinito; nessuno di essi, euclideo o non-euclideo, è in grado di includere tutte le dimensioni del colore. Qualcuno ha detto (Paul Klee?) che il colore sta in cima a una collina, per poterlo assediare e catturare, bisognerebbe salire la collina dall’una e dall’altra parte, contemporaneamente. Un doppio simultaneo tra opposti: impraticabile.
Lei lavora e riflette in un terreno al confine tra scienza, tecnica e grafica. Pensa che conoscere il colore dal punto di vista tecnico e scientifico possa essere utile al lavoro dell’artista?
Non so se e quanto, e per quanto tempo, il testo De la loi du contraste simultané des couleurs di Michel-Eugène Chevreul e le tecniche ottiche di tessitura abbiano inciso, in modo sostanziale, nella promozione della creatività artistica. Non particolarmente, secondo alcuni. Non ho competenza tecnica per dire della perenne questione del rapporto tra l’arte, la scienza e la tecnica. Naturalmente anche la conoscenza tecnica e scientifica accresce la cultura del colore e c’è interazione tra queste discipline, ma c’è anche specificità, come è già stato detto: la scienza lascia dimostrazioni, l’arte lascia tracce; solo ai livelli supremi, ai livelli meta-, le interazioni si completano nelle integrazioni. Faccio ancora un rimando, quasi una risonanza. In Teoria della forma e della figurazione Paul Klee – e Leonardo prima (Trattato della pittura, II, 42) –, trattando delle energie motrici, descrive e illustra il processo generativo del punto quale agente: il punto si mette in movimento e genera la retta, la retta il piano, il piano il volume. Sembra l’eco delle leggi di Keplero che governano l’armonia del mondo: i pianeti (il punto) descrivono attorno al sole delle ellissi (la linea); all’interno delle ellissi i relativi raggi vettori spazzano delle aree (le superfici); i quadrati (le superfici) dei tempi di percorrenza sono proporzionali ai cubi (volumi) dei semiassi maggiori di tali ellissi. È il processo descritto dalla prima, dalla seconda, dalla terza legge.
Senza alcuna presunzione didattica, penso che anche un percorso introduttivo a una cultura e a una pratica del colore possa procedere per momenti progredienti, quasi grammaticali:
– nominazione – ciascun colore è istruito in sé e per sé – punto
– declinazione – ciascun colore è seguito lungo le sue flessioni – linea
– coniugazione – ciascun colore è rapportato con ciascun altro colore – superficie
– sintassi – ciascun colore partecipa al volume o modello cromatico – volume
A questo proposito Josef Albers suggerisce che i sistemi, e i relativi modelli di colore, dovrebbero essere studiati al termine delle esperienze e delle pratiche percettive, non all’inizio, come di solito avviene.
Secondo lei si può elaborare una teoria dell’armonia dei colori?
Emanuele Severino nel suo Destino della necessità osserva che «nel terreno originario in cui cresce il linguaggio dell’Occidente» le parole che hanno nella loro radice una consonante liquida, “l” oppure “r”, portano il timbro della flessione, il timbro di ciò che il mortale può piegare, può disporre a un fine: vedi arte, arco, arto, colore ...
Stante questo approccio, poiché anche l’ar-monia porta nella sua radice il timbro della flessione, mi sembra che non si possa dare una teoria oggettuale e inflessibile dell’armonia, compresa quella dei colori; si possono avere teorie, scuole, movimenti, manifesti, piani ... a meno che non si tatti di un ambito ergonomico o di una specifica necessità.
Per quanto mi riguarda, nel tentativo di sfuggire alle insidie dell’armonia, mi sono limitato, in campo didattico, alle sole coniugazioni dei tre ordinari parametri percettivi del colore: la tinta, la chiarezza, la saturazione, dalle cui combinazioni e permutazioni due o più oggetti possono presentare cromaticamente:
– risonanza: concordanza di tutti e tre i parametri, nessuna discordanza – “1” caso
– consonanza: concordanza di due parametri, discordanza di un parametro – “3” casi
– assonanza: concordanza di un parametro, discordanza di due parametri – “3” casi
– dissonanza: discordanza di tutti e tre i parametri, nessuna concordanza – “1” caso
Ciascuno di questi “8” casi può essere disposto ai vertici di un cubo, di uno dei modelli più versatili e interdisciplinari. Ciascun parametro ha poi innumerevoli varianti, per cui il modello non pone alcun impedimento alla propria “armonia”.
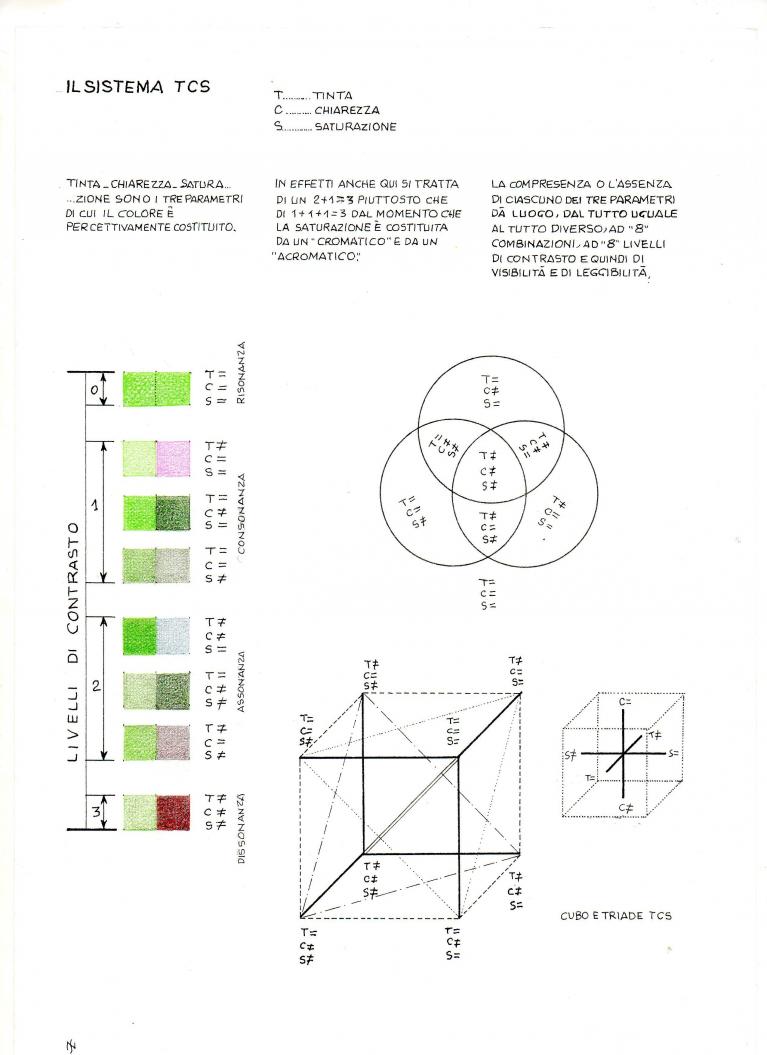 Sistema TCS
Sistema TCS
Cosa pensa della mistica del colore di Kandinskij?
Mi è difficile rispondere a questa domanda. Trovo però intrigante l’dea che Kandinskij ha del colore: ciascun colore, al momento stesso del suo apparire, del suo affacciarsi alla bocca del suo tubetto, manifesta già il proprio «principio di necessità interiore». Una necessità e un destino che risalgono al primordiale principio di polarità (Goethe). Così il giallo è, per sua necessità interiore, eccentrico e centrifugo, mentre il blu, suo contrappunto, è, per la stessa interità, concentrico e centripeto; ambedue mediati dal rosso, in equilibrio dinamico, e dal verde, in equilibrio statico. Il colore, come la forma, partecipa del principio di necessità interiore e colore e forma insieme muovono verso una sommità spirituale, come avviene nel triangolo e nella piramide, dove tutti i punti della base progrediscono, con una tensione mistica, verso un punto a loro esterno chiamato vertice. Il colore “estratto” e liberato dalla gravità dei corpi non è più imitazione, diventa “astratto" e può procedere per forza propria.
Per questo credo che la casa dei colori non siano gli oggetti o gli ambienti, ma i tubetti, le cartelle, i cataloghi, i campionari, gli atlanti, i modelli ..., quando i colori non sono ancora questo o quello, ma disponibili a questo e a quello.
Alla polarità nello spazio cromatico corrisponde, nello spazio proiettivo, la dualità tra il piano (l’estenso) e il punto (l’intenso), intermediati dalla retta (il tenso). I due poli di ciascuno dei due sistemi, quello cromatico e quello geometrico, sono tra loro coniugati da una lemniscata: una magnifica e singolare curva di Cassini a forma di 8 o anche di una circonferenza con la sua metà rigirata; una curva continua che con un nodo doppio, rosso e verde, lega due regioni, quella gialla e quella blu, due fuochi tra loro complementari.
Una curva, la lemniscata, onnipresente; è la traiettoria andata/ritorno dei cosmonauti in circumnavigazione, è la dualità chioma/radice degli alberi, è la complessa articolazione psico-motoria dell’uomo, anche limitandosi alla sola mano virtuosa del pianista in esecuzione: una coordinata catena di lemniscate embricate l’una con l’altra. La lemniscata è simbolo dell’infinito. Lo stesso cerchio dei colori di Kandinskij, a dispetto della sua apparente continuità geometrica, è un luogo di opposizioni, di polarità; metà concava e metà convessa, metrà discendente e metà ascendente. «I sei colori che, a coppie, formano tre grandi contrasti, si presentano a noi come un grande cerchio, come un serpente che si morde la coda (simbolo dell’infinito e dell’eternità). E alla destra e alla sinistra noi troviamo le due grandi possibilità del “silenzio”: il “silenzio” della nascita e il “silenzio” della morte (Vassilij Kandinskij). Una concezione vettoriale e non scalare.
Nel catalogo della Biennale del 1986 lei conclude la sua presentazione con l’etimo paradossale del termine colore: «colore vuol dire: celare e insieme rivelare». È vero, i colori ricoprono le cose, ma senza i colori non le vedremmo. Per lei quale dei due significati è prevalente?
La superficie, estrema regione dei corpi, è il luogo doppio dove il sottostante può rivelarsi, affiorando, oppure tenersi celato e remoto. Il carattere doppio delle superfici rimanda al carattere doppio delle linee quando Paul Klee distingue tra il «lineare attivo» e il «lineare passivo» e pone tra loro il «lineare medio». Si può azzardare l’opinione che il “rivelare” del colore è proprio del mondo vivente e il “celare” di quello non vivente? Forse è una distinzione troppo... superficiale. Una considerazione. Comunemente si usa dire, e anche illustrare, che in generale il colore degli oggetti risulterebbe dalla riflessione di una quota parte, selezionata, della luce che essi ricevono, ma le sorgenti “illuminanti” (sorgenti di 10 grado) non illuminano gli oggetti, ma li irradiano, li innescano, e questi, a loro volta, emettono una loro specifica radiazione visiva che noi chiamiamo “colore”. Dunque anche gli oggetti, se “irradiati”, sono sorgenti (sorgenti di 20 grado) e il loro colore rivela la loro costituzione materiale e strutturale.
D’altra parte, se il colore dei corpi risultasse da un’immediata riflessione selettiva della luce che essi ricevono, vorrebbe dire che la luce, su loro incidente, sarebbe costituita da un fascio di luce già colorata ma, come Newton espressamente sottolinea: «the rays are not coloured». (Qui il termine “luce” è detto in modo improprio ma abituale). Come può allora un colore, un colore, non una materia colorata, trattandosi di un’esperienza soggettiva, coprire un altro colore, celare il colore di un oggetto? I colori possono virare per sintesi o susseguirsi l’uno con l’altro, vedi ad esempio, la cosiddetta “fuga dei colori”: le post-immagini consecutive dopo l’osservazione di un’intensa sorgente luminosa “bianca”; oppure la trascolorazione di un materiale a seguito di un trattamento termico crescente, come nel caso della goethite (!): gialla all’inizio, poi arancione, rossa, marrone, bruna, nera.
Il colore di una superficie può invece essere attenuato e poi cancellato rendendola speculare o trasparente. Specularità e trasparenza sono le due estreme strategie con le quali un oggetto tenta di sottrarsi allo sguardo dell’osservatore. Ma la stessa lastra di vetro o la stessa superficie d’acqua, pur trasparenti se osservati frontalmente, diventano sempre più speculari man mano che lo sguardo diventa sempre più obliquo rispetto all’osservatore frontale; a questo punto la trasparenza e la specularità non appartengono più agli oggetti, ma sono rispediti all’osservatore, responsabile del proprio punto di vista.
Un altro ruolo primario svolto dal colore, nel celare e nel rivelare (rilevare) è quello dell’eguagliamento e del contrasto, del mimetismo e del risalto, tra le figure, tra gli oggetti e il loro intorno, un tema già oltremodo approfondito nella specifica letteratura (Giuseppe Di Napoli).
Si consideri anche un particolare caso di occultamento. I colori “magenta” (porpora) si differenziano dagli altri colori spettrali perché non hanno una loro specifica lunghezza d’onda denotativa e quando, nel diagramma di cromaticità CIE, debbano essere fisicamente designati, li si specifica con la denotazione dei loro contrari (complementari) verdi, preceduta dal segno meno (–). Trovo sorprendente che una cosa venga chiamata con il nome del suo contrario, utilizzando una doppia negazione (–) (–). Se ogni colore cela il proprio complementare vuol dire che, parallelo al nostro, c’è un altro mondo, quello dei “colori” assorbiti, che ha gli stessi nostri colori, solo diversamente riferirti: il sangue è turchese, i prati rosa, i “grandi cavalieri azzurri” di Franz Marc sono gialli tendenti all’arancione, sulla lavagna nera, con il gessetto bianco, il professore scrive, sul quaderno bianco, con l’inchiostro nero, gli studenti cancellano. Dovremmo allenarci, in tutti i sensi, alla dualità, come fanno i fotografi o i radiologi quando leggono, alla pari, i “positivi” e i “negativi”.
Mi sembra, in definitiva, che il colore possieda un doppio statuto: da una parte rivela il suo oggetto (estraversione), dall’altra cela il suo complementare (introversione): l’energia radiante assorbita. Il colore è un medium fluido: sta inquieto tra il velare e il ri-velare, sta in continua apprensione: come il vetro, come la sfera.
Un’ultima domanda, un po’ personale: lei si è occupato da sempre del colore fin dalla pubblicazione del libro Colore: codice e norma, scritto in collaborazione con Ave Tornaghi per Zanichelli nel 1981, un testo molto complesso che esamina il colore dal punto di vista scientifico e nelle applicazioni tecniche. Sono molto curiosa di sapere che cosa l’ha spinta a dedicare ai colori molta parte della sua ricerca.
Il Quaderno Colore: codice e norma riporta un numero limitato di esempi, sufficienti comunque a ricavare alcune considerazioni generali che riguardano la distinzione tra colore-segno e colore-segnale, la distinzione tra colori-norma (obbligati) e colori-codice (convenuti), la limitata portata dei colori quando si tratti di identificare con immediatezza e sicurezza numerose informazioni: diciamo 8÷10, la possibilità di tradurre valori numerici in codici cromatici; in quanto anche energia, il colore può essere impiegato per codificare, comunicare, condurre, decodificare, interpretare informazioni, come sistema trivariante può essere confrontato con altri sistemi trivarianti, può estendersi dal micro al mega: puoò figurare il sistema quark-antiquark o leggere e interpretare i colori delle stelle.
Per quanto poi riguarda il mio interesse per il colore, a dire il vero, non proviene da alcuna pregressa vocazione; ho avuto l’opportunità professionale nell’insegnamento di trattare due discipline: da una parte la geometria, dall’altra il colore e talvolta ho cercato, o immaginato, qualche risonanza tra le due. Ma forse c’è un movente più remoto: sono nato in un bel posto, nelle terre di Urbino, poi, per strada, ho incontrato persone, e lei è tra queste, creative e generose che mi hanno trasmesso il piacere dei nodi e delle intesezioni.
Grazie. Ho trovato le sue risposte molto affascinanti per il confronto tra lo spazio cromatico e lo spazio della geometria e per tutte le altre osservazioni fenomenologiche che ci invitano a guardare le cose con maggiore attenzione e a immaginare punti di vista insoliti.









